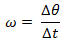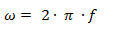PRIMERA
LEY DE NEWTON O LEY DE INERCIA (DELIA MORALES)
La primera ley del
movimiento rebate la idea aristotélica de que un cuerpo solo puede mantenerse
en movimiento si se le aplica una fuerza. Newton expone que:
“Corpus omne perseverare in
statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a
viribus impressis cogitur statum suum mutare”.
“Todo cuerpo continúa en su
estado de reposo o movimiento uniforme en línea recta, no muy lejos de las
fuerzas impresas a cambiar su posición”.
Esta ley postula, por tanto,
que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo
o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una
serie de fuerzas cuya resultante no sea nula. Newton toma en consideración,
así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas
de roce o fricción, que los frena de forma progresiva, algo novedoso respecto
de concepciones anteriores que entendían que el movimiento o la detención de un
cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero
nunca entendiendo como tal a la fricción.
En consecuencia, un cuerpo
que se desplaza con movimiento rectilíneo uniforme implica que no existe
ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no
se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de
los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta
cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.
Newton retomó la ley de la
inercia de Galileo: la tendencia de un objeto en movimiento a continuar
moviéndose en una línea recta, a menos que sufra la influencia de algo que le
desvíe de su camino. Newton supuso que si la Luna no salía disparada en línea
recta, según una línea tangencial a su órbita, se debía a la presencia de otra
fuerza que la empujaba en dirección a la Tierra, y que desviaba constantemente
su camino convirtiéndolo en un círculo. Newton llamó a esta fuerza gravedad y
creyó que actuaba a distancia. No hay nada que conecte físicamente la Tierra y
la Luna y sin embargo la Tierra está constantemente tirando de la Luna hacia
nosotros. Newton se sirvió de la tercera ley de Kepler y dedujo matemáticamente
la naturaleza de la fuerza de la gravedad. Demostró que la misma fuerza que
hacía caer una manzana sobre la Tierra mantenía a la Luna en su órbita.
La primera ley de Newton
establece la equivalencia entre el estado de reposo y de movimiento rectilíneo
uniforme. Supongamos un sistema de referencia S y otro S´ que se desplaza
respecto del primero a una velocidad constante. Si sobre una partícula en
reposo en el sistema S´ no actúa una fuerza neta, su estado de movimiento no
cambiará y permanecerá en reposo respecto del sistema S´ y con movimiento
rectilíneo uniforme respecto del sistema S. La primera ley de Newton se
satisface en ambos sistemas de referencia. A estos sistemas en los que se
satisfacen las leyes de Newton se les da el nombre de sistemas de referencia
inerciales. Ningún sistema de referencia inercial tiene preferencia sobre otro
sistema inercial, son equivalentes: este concepto constituye el principio de
relatividad de Galileo o newtoniano.
El enunciado fundamental que
podemos extraer de la ley de Newton es que:
Esta expresión es una
ecuación vectorial, ya que las fuerzas llevan dirección y sentido. Por otra
parte, cabe destacar que la variación con la que varía la velocidad corresponde
a la aceleración.
SISTEMAS
DE REFERENCIA INERCIALES
La primera ley de Newton
sirve para definir un tipo especial de sistemas de referencia conocidos como
sistemas de referencia inerciales, que son aquellos desde los que se observa
que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad
constante.
Un sistema de referencia con
aceleración (y la aceleración normal de un sistema rotatorio se incluye en esta
definición) no es un sistema inercial, y la observación de una partícula en
reposo en el propio sistema no satisfará las leyes de Newton (puesto que se
observará aceleración sin la presencia de fuerza neta alguna). Se denominan
sistemas de referencia no inerciales.
Diferencia de planteamiento
de un problema debido a la posibilidad de observarlo desde dos puntos de vista:
el punto de vista de un observador externo (inercial) o desde un observador
interno
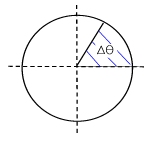
Por ejemplo considérese una
plataforma girando con velocidad constante, ω, en la que un objeto está atado
al eje de giro mediante una cuerda, y supongamos dos observadores, uno inercial
externo a la plataforma y otro no inercial situado sobre ella.
Observador inercial: desde
su punto de vista el bloque se mueve en círculo con velocidad v y está
acelerado hacia el centro de la plataforma con una aceleración centrípeta. Esta
aceleración es consecuencia de la fuerza ejercida por la tensión de la cuerda.
Observador no inercial: para
el observador que gira con la plataforma el objeto está en reposo, a = 0. Es
decir, observa una fuerza ficticia que contrarresta la tensión para que no haya
aceleración centrípeta. Esa fuerza debe ser. Este observador siente la fuerza
como si fuera perfectamente real, aunque solo sea la consecuencia de la
aceleración del sistema de referencia en que se encuentra.
En realidad, es imposible
encontrar un sistema de referencia inercial, ya que siempre hay algún tipo de
fuerzas actuando sobre los cuerpos; no obstante, siempre es posible encontrar
un sistema de referencia en el que el problema que estemos estudiando se pueda
tratar como si estuviésemos en un sistema inercial. En muchos casos, la Tierra
es una buena aproximación de sistema inercial, ya que a pesar de contar con una
aceleración traslacional y otra rotacional, ambas son del orden de 0.01 m/s² y,
en consecuencia, podemos considerar que un sistema de referencia de un
observador en la superficie terrestre es un sistema de referencia inercial.
APLICACIÓN
DE LA PRIMERA LEY DE NEWTON
Se puede considerar como
ejemplo ilustrativo de esta primera ley o ley de la inercia una bola atada a
una cuerda, de modo que la bola gira siguiendo una trayectoria circular. Debido
a la fuerza centrípeta de la cuerda (tensión), la masa sigue la trayectoria
circular, pero si en algún momento la cuerda se rompiese, la bola tomaría una
trayectoria rectilínea en la dirección de la velocidad que tenía la bola en el
instante de rotura.
Tras la rotura, la fuerza neta ejercida sobre la bola es 0, por lo que experimentará, como resultado de un estado de reposo, un movimiento rectilíneo uniforme.
SEGUNDA LEY DE NEWTON
También conocida como Ley Fundamental de la Dinámica, es la que determina una relación proporcional entre fuerza y variación de la cantidad de movimiento o momento lineal de un cuerpo. Dicho de otra forma, la fuerza es directamente proporcional a la masa y a la aceleración de un cuerpo.
EJEMPLOS:
VIDEO
https://www.google.com/url?sa=t&source=web&rct=j&url=https://m.youtube.com/watch%3Fv%3DKx9ggQMtexo&ved=2ahUKEwiRq8CozKXoAhXIdd8KHV4sDcoQtwIwAHoECAIQAQ&usg=AOvVaw3Uq7rph7BApmpbnbkAgic6&cshid=1584585028849
JUANA FABIOLA SAQUIC VASQUEZ
TERCERA LEY DE NEWTON
"Luisa Gomez"
La Tercera Ley de Newton también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Explicación
En términos más explícitos: La tercera ley expone que por cada fuerza que actúa sobre un cuerpo, éste realiza una fuerza de igual intensidad y dirección pero de sentido contrario sobre el cuerpo que la produjo.
Dicho de otra forma, las fuerzas siempre se presentan en pares de igual magnitud, sentido opuesto y están situadas sobre la misma recta. Matemáticamente la tercera ley del movimiento de Newton suele expresarse como sigue: F1 = F2' Por lo que,F1 es la fuerza que actúa sobre el cuerpo 1 y F2' la fuerza reactiva que actúa sobre el cuerpo 2.
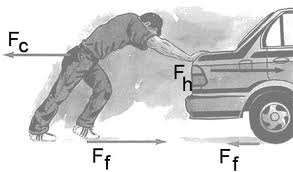
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando empujamos a una persona,un automóvil, etc , nosotros también nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona o el automóvil hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actúan sobre cuerpos distintos.
Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".
Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley de Newton
EJEMPLOS
https://www.google.com/url?sa=t&source=web&rct=j&url=https://www.youtube.com/watch%3Fv%3DVJXNWNEQ75o&ved=2ahUKEwiW0NmAk6joAhUEJKwKHeooDHAQo7QBMAF6BAgAEAQ&usg=AOvVaw0TpJFC1Y2dfcQI6-eDKSgN